Xiaoxu Meng

 

• sequence classification
• sequence prediction
• seq2seq(https://www.csdn.net/article/2015-08-28/2825569)
  • Input: sentence
  • Output: sentence
  • pinput -> intermediate state -> output (see the reference)
  • encoder:
  • decoder:
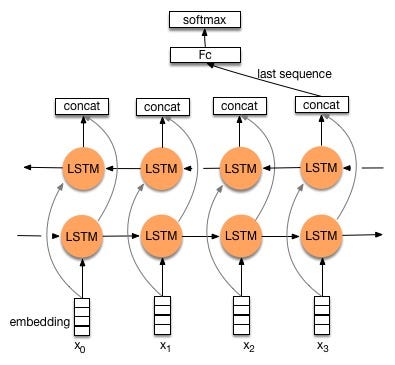
• Bidirectional LSTM
  • 

 

Collection of all pre-trained Word2Vec Models:

http://ahogrammer.com/2017/01/20/the-list-of-pretrained-word-embeddings/

Google’s model seems not reliable…

Here are some similarity tests of Google’s model:

The similarity between good and great is: 0.7291509541564205
The similarity between good and awesome is: 0.5240075080190216
The similarity between good and best is: 0.5467195232933185
The similarity between good and better is: 0.6120728804252082
The similarity between great and awesome is: 0.6510506701964475
The similarity between great and best is: 0.5216033921316416
The similarity between great and better is: 0.43074460922502006
The similarity between awesome and best is: 0.3584938663818339
The similarity between awesome and better is: 0.27186951236001483
The similarity between best and better is: 0.5226434484898708
The similarity between food and foodie is: 0.3837408842876883
The similarity between food and eat is: 0.5037572298482941
The similarity between foodie and eat is: 0.3050075692941569
The similarity between park and view is: 0.1288395798972001
The similarity between design and art is: 0.3347430713890944

• Information about midterm
• PCFG
  • Start with S
  • ∑Pr(A -> gamma | A) = 1
    • (conditional) probability of each item has to sum to one
  • Pr(O = o1,o2,…,on|µ)
    • HMM: Forward
    • PCFG: Inside-Outside
  • Guess Pr: argmax_(Z)[ Pr(Z|O, µ) ]
    • HMM:Use Viterbi to get
    • PCFG: Use Viterbi CKY to get
    • *Z is the best sequence of states
  • Guess µ: argmax_(µ)[Pr(O|µ)]
    • HMM:Use forward-backward to get
    • PCFG: Use Inside-outside to get
  • Example:
    • Sentence:
      • ——————-S
      • ——–NP—————-VP
      • ——–NP———-V————-NP
      • ——people——eats —–adj——–N
      • —————————roasted—-peanuts
    • Problem:
      • Pr_µ(peanuts eat roasted people) = Pr_µ(people eat roasted peanut)
    • We can try to generate head of each phrase:
      • ————————————S (Head: eat)
      • ——–NP(Head: people)—————————–VP(Head: eat)
      • ——–NP(Head: people)———-V(Head: eat)——————————–NP(Head: peanut)
      • ——people(Head: people)——eats(Head: eat)————-adj(Head: N/A)—————–N(Head: peanut)
      • —————————————————————–roasted(Head: N/A)————-peanuts(Head: peanut)
    • Should have: Pr[S (Head: eat) -> NP(Head: people) VP(Head: eat)] > Pr[ S (Head: eat) -> NP(Head: peanut) VP(Head: eat) ]
  • Dependency representation:
    • Sentence:
      • —————————eat
      • —————people—————peanuts
      • —————–the—————–roasted
    • Lexical (bottom up)
    • NP ->det N
• Evaluation
  • Reference Reading:How Evaluation Guides AI Research
    • Intrinsic evaluation
    • Extrinsic evaluation
  • Kappa’s evaluation
  • Metric: precision recall
  • How to evaluate two structures which could generate the same sentence?
    • Answer: Generate more than one output for each input, convert the output into set of output, and use precision and recall to measure.
  • Reader evaluation:
    • If the reader’s score agree with the machine, stop
    • else: let another reader read the essay

Questions:

1. Generative Model P(X,Y)
2. Discriminative model P(Y|X)

MainPoints

1. Block sampler: Instead of sample one element at a time, we can sample a batch of samples in Gibbs Sampling.
2. Lag and Burn-in: can be viewed as parameters (we can control the number of iterations)
   1. lag: mark some iterations in the loop as lag, then throw away the lag iterations, then the other samples become independent.
      1. Example: run 1000 iters -> run 100 lags -> run 1000 iters -> 100 lags …
   2. burn in: throw away the initial 10 or 20 iterations (burn-in iterations), where the model has not converged.
      1. The right way is to test whether the model has converged.
3. Topic model:
4. The sum of the parameter of each word in a topic doesn’t need to be one
5. The derivative (branches) of LDA (Non-parametric model):
   1. Supervised LDA
   2. Chinese restaurant process (CRP)
   3. Hierarchy models
      1. example: SHLDA
      2. gun-safety (Clinton) &  gun-control (Trump)

Parsing:

Any context which can be processed with FSA can be processed with CFGs. But not vice versa.

?	turning machine
	(Don’t cover in this lecture)
CSL	Tree adjusting Grammar	PTAGs
	(Don’t cover in this lecture)
CF	PDA/CFGs	PCFGs
	PDA/CFGs Allow some negative examples. And can handle some cases that cannot be processed by FSA. For example: S -> aSb {a^nb^n} cannot be processed by FSA because we need to know the variable n. But FSM only remember the states, it cannot count.
Regular	FSA/regular expressions	HMM

Example1:

The rat that the cat that the dog bit chased died.

Example2:

Sentence: The tall man loves Mary.

————-loves

—–man————Mary

-The——tall

Structure:

——————-S

——–NP——————VP

—DT-Adj—N             V——–NP

—the-tall–man       loves—–Mary

Example3: CKY Algorithm

0 The 1 tall 2 man 3 loves 4 Mary 5

[w, i, j] A->w \in G

[A, i, j]

Chart (bottom up parsing algorithm):

0 The 1 tall 2 man 3 loves 4 Mary 5

–Det —— N ———V ——NP—-

———–NP ———–VP ———

—————- S ———————

Then I have:

[B, i, j]

[C, j, k]

So I can have:

A->BC : [A, i, k] # BC are non-determinal phrases

NP ->Det N

VP -> V NP

S -> NP VP

Example4:

I      saw         the        man       in        the       park        with      a       telescope.

——————– NP—————– PP ———–

–                         —————NP———————

————————NP—————————–

 

A->B . CD

B: already

CD: predicted

[A -> a*ß, j]

[0, S’-> *S, 0]

scan: make progress through rules.

[i, A -> a* (w_j+1) ß, j]

A [the tall] B*C

i, [the tall], j

Prediction: top-down prediction B-> γ

[i, A-> a * Bß, j]

[j, B->*γ, j]

 

Combine

Complete (move the dot):

[i, A->a*ß, k] [k, B->γ, j]

 

I                          k                       j

–[A->a*Bß]———[B->γ*]—–

 

Then I have:

[I, A->aB*ß, k]

• • watch the new talk and write summary
  • Noah Smith: squash network
  • Main points:
    • difference between LSA & SVD
    • Bayesian graphical models
      • informative priors are useful in the model
    • Bayesian network
      • DAG
      • X1X2…Xn
      • Po(X1, X2, …, Xn)
      • Generative story: HMM (dependencies)
      • A and B are conditionally independent given C iff P(A,B|C) = P(A|C) * P(B|C)
        •       C (to A, to B)
        •   A                             B
      • Example:
        •               Cloudy (to Sprinter and rain)
        • Sprintder(to wet grass)                   Rain (to wet grass)
        •                       Wet grass(final state)
        • w’s are observable
        • State change graph:  π -> S1 -> S2 -> S3 -> … -> St
        • w’s are observable
          • μ~(A,B,π)
          • Have a initial π for C, π~Beta(Gamma(π1), Gamma(π2))
          • C is Bernoulli (π)
          • S~ Bernoulli(π(S | C))
          • R~Bernoulli(π(S | C))
          • W ~ Bernoulli(\tao (ω | S,R))
          • π~Dirichlet(1)
          • S1~Cat(π)S2~Cat(a_s1,1  ,  a_s1,2  ,   ….  ,   a_(s1,n))* Cat is chosen from the transition matrix
          • ω1~Cat(b_s1,1  ,  b_s1,2  ,   ….  ,   b_(s1,n))ω2~Cat(b_s1,1  ,  b_s1,2  ,   ….  ,   b_(s1,n))* Cat is chosen from the transition matrix
      • What just been introduced is the unigram model, here is the bigram model
      • 
      • P(s1, s2, …. , sn) = P(s1) P(s2|s1) P(s3|s1,s2) P(s4|s2,s3)..
      • For EM, we need to recalculate everything, conditional distribution are different
    • Some distributions:
      • Binomial vs. Bernoulli
      • Multinomial vs. discrete / categorical
  • Document squashing

  Continue reading Lecture 5: Reduced-dimensionality representations for documents: Gibbs sampling and topic models